Exploring High-Dimensional Data Sets in Football: Topological Data Analysis

Data mining has revolutionised the world of business. The increasing availability of data combined with the globalisation of markets means that the discovery of the smallest competitive advantage can produce millionaire returns. The business of football could not be left behind.

On the playing field, footballers perform thousands of actions per game. Companies specialized in providing football statistics such as OPTA or Prozone employ an army of ‘data inputters’ who for meagre compensation jump at the opportunity to make a living by watching video after video of football matches and recording as many events as possible. For each player in each match they log the amount of times he passed the ball (with each leg of course), the amount of times he touched the ball, how many times he took a throw in or how many times he controlled on his left thigh. Literally thousands of events are logged.

These companies then sell massive statistical packages to the clubs, who while recognising the need to try and obtain competitive advantage from this new wave of information, are still mostly in the dark on how precisely to do this.

It’s simple to envisage extracting information from a single statistic. A typical process a football fan performs is looking at the leading goalscorers chart and assume that by seeing which strikers have scored the most goals something can be said regarding their quality.

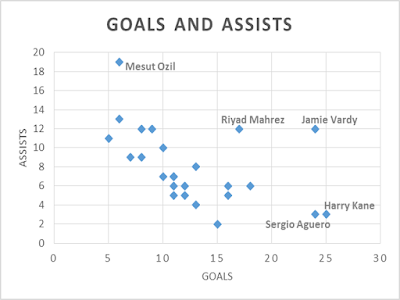
What happens when we have two statistics? Again, it doesn’t seem too difficult. Consider the table where the 25 players with the highest ‘goals+assists’ value for the 2015-16 Premier League season are displayed:

Note: As a caveat, the postponed Manchester United vs. Bournemouth game hasn’t been played at the time of writing, so any goals scored in that match aren’t reflected in the table. Should Manchester United beat Bournemouth by the 19 goal margin needed to classify for the Champions League next season, surely at least one of their players will make the top 25. Interestingly, only 5 other teams aren’t represented in this table: West Brom, Crystal Palace, Bournemouth, Norwich and Aston Villa; averaging amongst them a 16.8^th league finish (West Brom finished highest of these at 14) to Manchester United’s 5^th or 6^th.

Once again we can easily imagine extracting information from this ‘two dimensional’ data. We can differentiate three types of players which contribute to this total goals value: Players who score a lot but don’t assist much like Aguero and Kane, players who assist a lot but don’t score much like Ozil, or players that contribute in both items like the surprising Mahrez and Vardy of Leicester City. It’s a simple conclusion, almost trivial. The representation of data in two dimensions leaves information there for the taking, extremely available. The analytical process of interpreting this type of information and extracting concrete meaning is extremely natural for us.

What happens then when we have over 200 statistics? OPTA in association with Manchester City made a database for the 2011-12 Premier League season available to the general public, in which they collect over 200 in-game statistics for each player in each match of that season. Can we extract information or meaning in the same way from this type of data?

Topological Data Analysis (TDA) is a mathematic tool whose broad objective is precisely that: extracting qualitative information and meaning from high-dimensional data. It has been previously used for example to successfully analyse genetic data from cancer patients and discover patterns amongst groups of survivors. The key concept is perceiving the data as being located in a 200 dimensional space. This may seem overwhelming, but it’s actually quite natural. In the ‘goals+assists’ example, each player could be seen as a point in the plane, with two coordinates. If we had added a third statistic, like ‘passes’ for instance, each player could then be seen as a point in three dimensional space with its three coordinates (goals, assists and passes). This conceptualisation can be extrapolated to spaces with 200 coordinates, and there is an area of pure mathematics dedicated to describe geometric notions such as shape, closeness, regions, etc. in these spaces.

By applying TDA to a data set, the result is a two-dimensional representation as a graph of the originally high-dimensional data, where each node represents a grouping of the data points and vertices are determined in such a way that the distances and shape of the data in its original high-dimensional space is conserved under certain parameters in its new visual representation. By looking at the result we can deduce certain information regarding the original layout of the high-dimensional data. The mathematical detail of the method is actually quite technical, but the important property to keep in mind is that the representation in the form of a graph carries through some basic geometrical property of the data set.

The following images show the application of TDA to the database made public by OPTA:

Each node represents a group of players, whose colour is determined by their playing position as the legend indicates. We can observe at first sight how the “geometry” of the more than 200 coordinates recognises different playing positions and styles of play between the players. It can differentiate clearly between defenders, midfielders and strikers; and can even differentiate between more specific subcategories as the ones we have circled. The same graph can be “coloured” according to different parameters:

For this image, each node has the colour corresponding to the final position in the league table for which the players which compose it play. Once again, we can appreciate that this information is available in the geometry of the coordinates, because nodes of different colours appear in different ‘regions’ of the graph instead of being mixed up. This means that there is something in the combination of all the considered statistics of players from “top” teams that set them apart from players from “lesser” teams. Assuming that in a league as sophisticated as the Premier League, differentiating between the quality of the team is synonymous with differentiating between the quality of the players, we can began to anticipate the potential that discovering this type of information has when applied to young players from unknown leagues with view of better informing a club’s recruitment strategy.

This last point is important: this methodology allows us to detect which qualities are supported by the information contained in the “geometric layout” of the more than 200 statistics we are considering simultaneously. The next example can illustrate this point further:

This graph is the result of applying the technique to a slightly different dataset, where each node is composed by an entire team’s performance for a match, rather than looking at each player individually. We can appreciate that of the two colourings, the one on the left (final position in the league table of that team) appears to be much less ‘mixed up’ when compared to the one on the right (the specific result of that match). While the performances from “top” teams occurs in certain ‘areas’ or ‘zones’ of the 200-dimension space, the same cannot be stated for performances that ended in victory for example, which occur mixed up with performances leading to draws or defeats. This is interpreted as follows: while the information about a team’s quality (seen as its final position in the league table) is ‘codified’ inside the combination of the considered statistics and can be found in its geometric layout (which data points are close to which others), the same cannot be said of a match’s specific result. The considered statistics cannot accurately predict what the final result of a match will be; this can be due to the chance of a penalty or hitting the woodwork. What it can ‘predict’ is the final league position of a team; this underlying information of “performance quality” is mostly available when analysing in-game statistics.

Other types of relevant conclusions can be drawn out from applying this methodology; for example the fact that for the 2011-12 season Chelsea and Fulham (6^th and 9^th) employed a similar style of play.

This type of information proves to be very important for football because it establishes the existence of middle ground for the massive collection of data to meet with ‘footballistically’ valuable applications. We have established that there are techniques that can take advantage of large data sets which can seem overwhelming and useless for traditional analytical methods, and the information extracted can be used to revolutionise exciting areas of football such as player recruitment and talent identification.